You can create Spatial ACIS® objects with the help of ODA’s B-Rep Builder however if certain things are not taken into account, an incorrect ACIS object can be created. To prevent this, a validator (BB validator) is included in the B-Rep Builder.
What is the validator? BB validator is an object that checks the input data used to create an ACIS object for the presence of errors and some features characteristic of the ACIS core. By default BB validator is enabled. Disabling it is not recommended because there is the probability that a created object may contain errors, but you can disable it by calling this method:
void OdBrepBuilderBase::enableValidator(false)
Let's go through the checks performed by BB validator. All explanations are in terms of B-Rep. As you know, to create a face, in general, you need a surface bounded by some kind of loop.
First, the validator checks if the loop is correctly set. This is done using several checks, and the first one checks if coedges are specified in the loop. That is, if there is at least one coedge in the loop. If not, it throws the eNoTrimmigLoop exception.
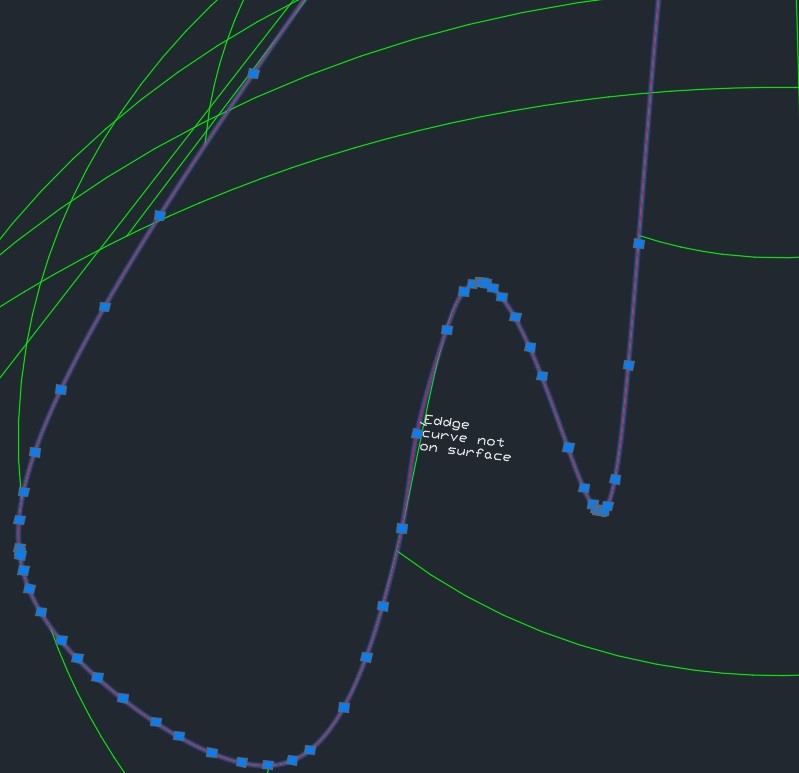
The next check determines whether the loop is on the surface. The method in which it is done is bool BrepBuilderValidator::isTrimmingLoopOnFaceCheck(double dTol). If the distance is greater than a given distance, it is considered that the curve, and therefore the loop, is not on the face and the exception eLoopIsNotOnFace is raised. The algorithm is iterated over coedges into a loop; from the current edge it takes twenty points, and for each point it assumes that it is on the surface. If so, when we define the corresponding 2D point in the parametric space of the surface and then calculate the 3D point on the surface, it should coincide with the point on the 3D curve at the edge. If the distance between them is less than the tolerance, it iterates to the next 3D point of the edge.
The next images shows a cone surface with a subtracted pole. Blue is the edge, and red indicates the zoomed edge (see second image).
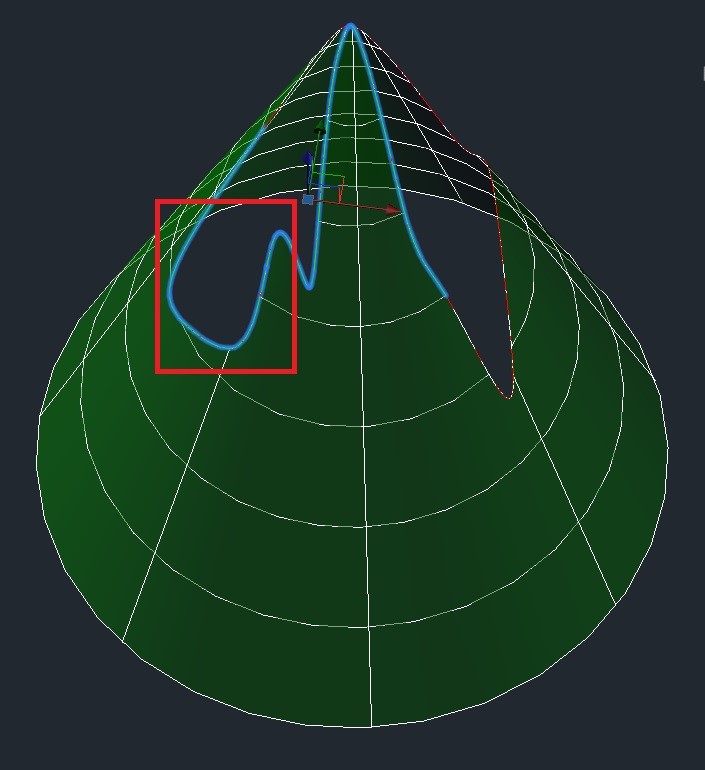
This second image shows the zoomed area. One of the points of the edge is not on the surface, which will be an error.
If the coedge is defined by a parametric curve, the validator takes twenty 2D points, and it determines the associated 3D points on the surface. It is assumed that these points lie on the 3D curve at the edge. This means that if you define parameters corresponding to them, and then again calculate 3D points using them, they must coincide within a tolerance. If this is not the case, the exception eLoopIsNotOnFace is raised.
As you can see, BB validator uses parametric curves. In this case, an important thing is that the intervals of parametric curves and 3D curves must match. This must be taken into account when working with ACIS, B-Rep Builder, and the BB validator: there is a check that the interval of the parametric curve must be equal or include the interval of the 3D curve. This check is performed in the bool AcisBBValidator::isDir2dCoincide3d(double dTol) method. So if we order a few 2D points, for example p1, p2, p3, we obtain on the surface the corresponding 3D points pp1, pp2, pp3 and points on the 3D curve c1, c2, c3. Geometrically, the order of points on the surface should be the same as a point on the 3D curve.
The next prerequisite is that the loop must be inseparable and closed. This is verified in bool BrepBuilderValidator::isTrimmingContinuousAndClosedCheck(double dTol). Here, checks are performed so that the end of the last edge coincides with the beginning of the first (taking into account the direction) and this condition is fulfilled for two adjacent edges (the current and the next).
There are several conditions for faces in ACIS: they cannot have zero area or more than one external loop. These conditions are checked in the BB validator using these methods:
- bool AcisBBValidator::checkZeroFaces(OdArray<BRepBuilderGeometryId> &arrZeroAreaFaces, double dTol)
- bool BrepBuilderValidator::checkNOuterLoops(double dTol)
Determining the number of external loops is still under development for closed surfaces due to the complexity of the algorithm.
The last check is implemented in the method bool AcisBBValidator::checkEdgeStartEndParam(double dTol). It checks the distance between the curve and the curve closest to the edge's start vertex. If the distance is greater than "tol", an exception eInvalidInput is raised.


